3 Déterminer les coordonnées du point dintersection de Cf et de laxe des ordonnées. 4 Dresser le tableau de variation de f puis donner lallure de Cf en mettant en évidence les résultats des questions précédentes dans le repère ci-dessous.
Forme Canonique D Une Fonction Polynome De Degre 2
La forme canonique est donc bien.
Determiner forme canonique graphiquement. Daprès mes souvenirs du lycée pour déterminer graphiquement léquation dune parabole on regarde les coordonnées du sommet de la parabole pour pouvoir en écrire la forme canonique. La forme canonique de lexpression A x ax bx c 2 est du type. La forme canonique dune fonction étant.
Lorsquune fonction est sous cette forme les coordonnées du sommet sont ℎ. Ax- 2 Avec labscisse du sommet de la parabole et lordonnée. Ensuite on calcule les valeurs de α et β à laide des formules de cours.
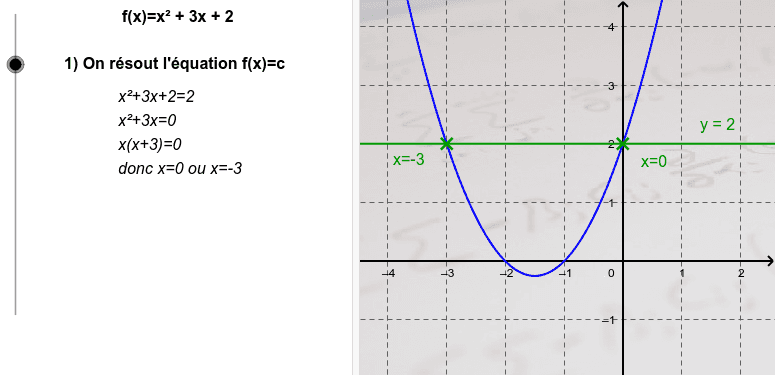
Graphiquement les solutions de lequation fx 0 sont les abscisses des points dintersection de la parabole et de laxe des abscisses. A 23 b 310 c 2 31. Forall x inmathbb R fleft xright3x2-12x18.
Forme canonique courbe variations. Forme canonique dun trinôme du second degré Tout trinôme du second degré de la forme où et désignent des réels avec peut sécrire sous sa forme canonique unique. Ici C est sous forme canonique.
Exercices corrigés de mathématiques pour les 1S sur le second degré. La seule différence est quon ne va pas regarder le b². Ces valeurs sont calculées à partir des valeurs a b et c de la forme développée de la fonction.
Il faut determiner en premier lieu la forme canonique de f puis utiliser si cela est possible la troisieme identite remarquable a2 b2 abab pour factoriser. 1 La forme canonique de la fonction f est fxax-alpha2Bêta a Déterminer graphiquement les valeurs de alpha et bêta b Déterminer graphiquement f1 et en déduire la valeur de a c Donner alors la forme canonique de la fonction f dDéterminer de même la forme canonique de la fonction g. 2 En déduire que pour tout réel on a D1.
Dans cette vidéo tu pourras comprendre comment lire graphiquement les différentes écritures possibles pour une fonction du second degré. 1 On pose 22 et 2 43. La forme canonique est fx a x - alpha² betaElle permet instantanément de connaître la représentation graphique de la fonction polynôme de second degr.
A TD02 SYSTEMES ASSERVIS CORRECTION Exercice 1. F x 0. La forme canonique dune fonction du second degré est 𝑦 𝑎 𝑥 ℎ 𝑘 𝑎 0.
On considère la fonction trinôme du second degré définie sur mathbb R par. F x x 1 2 0. Ensuite reste à déterminer a.
Donc je mintéresse à la forme canonique. Forme canonique facile Le principe va ressembler à ce quon a fait dans lexemple précédent. Donner en la retrouvant par le calcul la forme canonique de f.
Dans un premier temps on détermine les valeurs de a b et c. FONCTION DE TRANSFERT Question 1. On va vérifier quil sagit bien de la forme canonique.
Pour les transformer en leur forme canonique on utilise alpha et bêta. Cette forme sappelle la forme canonique. 3 Déterminer 1 4 A laide des informations précédentes déterminer la forme canonique de puis sa forme développée.
Puisque la forme canonique peut sécrire fx ax -x s 2 - y s on peut chercher les coordonnées du sommet de la parabole x s. Il est particulièrement facile sous forme canonique de déterminer les coordonnées du sommet du graphique. Déterminer sous forme canonique les fonctions de transfert des systèmes modélisés par les équations différentielles ci-dessous.
Y s Pour cela on cherche à résoudre léquation suivante. Sans utiliser la formule ci-dessus on a. 1 Déterminer la forme canonique de f.
Déterminer lexpression développée de la fonction trinôme f représentée dans un repère orthogonal par la parabole ci dessous. En déduire pour ha une le gain statique la lasse et lordre du système. A 4 86 b 5 10120 c 41 d 21 e 9 65 f 9 310 g 5 35 h 16 43 Exercice 2 Factoriser les expressions suivantes.
Notre calculateur en ligne vous permet de trouver instantanément les valeurs dalpha et bêta sur base de la forme développée de la fonction et donc de connaître sa forme canonique. Reconnaître une forme canonique à partir dun graphique - Corrigés dexercices Fonctions polynomiales et fonctions homographiques Mathématiques. F x x 2 4 x.
Variations extremum propriété de la courbe position relative Exercice 1. Donner la forme canonique des trois trinômes du second degré suivants. B 2.
Déterminer les formes canoniques de et. 2 b a α et 2 4 4 b ac a β On peut maintenant mettre A sous forme canonique en remplaçant α et β par. La forme canonique de f est fxax-alpha2beta avec alpha2 et beta-8 donc fxax-22-8 Le point de coordonnées 08 appartient à la courbe C_f.
Trouver la forme canonique Pour déterminer la forme canonique il suffit de trouver α et β Méthode 1 Si lon connait la valeur de x pour laquelle la fonction atteint un extremum grâce au tableau de variation ou à la courbe alors on peut en déduire directement α et β. Quel est le coefficient directeur. Ax ax α β 2 Que faire.
On peut toujours trouver la forme développée et canonique. Commençons par écrire la fonction f sous sa forme canonique. 1 2 3 Rappel.
En fait une expression polynomiale avec des x de second degré avec des x² est presque. Forme canonique forme factorisée étude graphique résolution déquations. A laide dune technique de calcul précise on sait déterminer la forme canonique dun trinôme du second degré.
α b 2 a 2 2 1 et β f 1 1 2 2 1 1 0. 1 Les CI sont nulles. F x x 2 2 x 1.
Comment trouver une forme canonique à partir dun graphique. Représenter graphiquement la fonction f définie sur par fxx24x. Daprès la représentation graphique de f on remarque que le sommet de la représentation graphique de f est atteint aux coordonnées -1.
F x x 1 2.























